Figure 1: My CIV102 team's bridge after buckling due to shear.

The "Bridge of unyielding Passive Aggression" was a bridge designed completely of matboard and cement glue by my CIV team (Ryan Qian, Kaden Seto, Alisha Ali, John Chen) for the CIV102 course project. This project was a unique engineering experience, working not under the constraints of feasability and knowledge of first years, but instead a materials and tools constraint. The goal of this project was to design 1 meter bridge that could withstand the greatest amount of load possible. Throughout this project, my team used iterative modification to diverge to different designs, truss load models to represent the load abilities of a design, and theoretical testing to evaluate and converge designs. Throughout this page we will discuss the effectiveness of these specific CTMFs in the context of the CIV bridge, and future applicability of these CTMFs.

The first step of creating a unique design was to diverge different designs. With such a complicated topic, it was difficult to intuitively understand what the best design is. Thus our approach to diverging was using iterative modification. In Figure 2, we can see the differing values following the first iteration of the team's bridge, which was to add a layer to the deck. This technique can also be described as the "M" from SCAMPER, however I have referred to it as "iterative modification" to recognize the importance of the iterative process with this tool. As the bridge was able to fail in 6 different ways, it was essential iterate a myriad of designs, and identify the strengths and weaknesses of each design. This tool was effective given the context of the project, as given our lack of experience in CIV we were able to understand how to improve designs slowly through iteration. This tool was effective while working within ignorance, however I'm sure that other diverging frameworks could provide more value in different contexts. Furthermore, I would like to acknowledge that this tool was likely useful given the objective of the design was optimization, rather than innovation. Thus, I would limit future usage of this design to optimization focused projects, with teams lacking in experience of the given field.

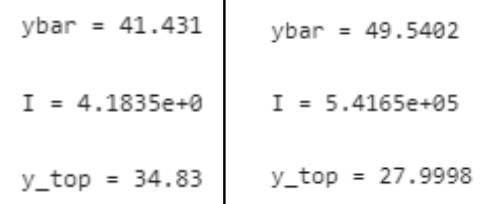
Figure 2: Geometry values before and after the first iteration of the bridge. On the left is the original bridge design and on the right is after the iteration.

The truss load model was used to represent the load abilities of the bridge. An example of model being used with initial design can be see seen in Figure 3. The model was resourcefully constructed using the newly taught matlab skills in ESC103. This model was used as a visualization of failure and the differing integrities in context of different failure types. The context of this CMTF, is simply a generalization of a visual representation of the limits of the design. This model was useful in the context of creating a bridge, as due to the modelling constraints, when adjusting a design to strength in relation to one failure type, other failure types will often weaken. Furthermore, with the context of the brute-force iterative diverging approach, the load graphs were especially useful in visualizing the effects and strengths of adjusting certain parameters. In future design works, this tool of visualizing the limits of a design will likely not be as useful when applied to non-constrained designs. For example, in the context of a design for comfortability of a backpack, this would be useless. Nonetheless, this tool served a valuable purpose in the context of the bridge design, and can likely still be applied to specific future design works.

Figure 3: 6 Graphs representing the load failure in each of the 6 different failure cases. To read graphs individually please zoom in.

When using an iteratively intensive diverging approach, it is essential to have a converging tool that can quickly evaluate the designs. Using the resourcefully created matlab program, we calculated the factor of safety in each mode of failure against each design. An example, of converging away from suboptimal designs is show in Figure 4. This method of converging was essential when creating the bridge, as we could not prototype and test designs due to the material constraints. Thus, theoretical testing was an essential tool in context of the project. Furthermore, we were able to quickly identify the strength of designs and compare using this tool. This tool was especially useful in this project, however we must acknowledge once again that this project was rooted in optimizing failure under constraints, thus this was unusually useful. When working with more open-ended designs, with less quantifiable metrics, or many metrics which are difficult to compare, this tool could become much less useful. Thus, I would limit the usage of this tool to projects with simple quantifiable metrics, especially those rooted in optimization.

Figure 4: The results of the factor of safety calculations for the bridge prior to the 9th iteration and after. the calculations were done using a load of 400N. On the left is prior to the iteration and on the right is after the iteration. The optimal design converged to the right design as it had a higher lowest factor of safety.